Big-O 표기법

알고리즘 평가

1 ~ N 까지의 합을 보여주는 두 알고리즘을 작성했다.

function addUpTo(n) {
    total = 0;
    for i to n total += i;

    return total;
}

function addUpTo2(n) {
    return n * (n + 1) / 2;
}

이 두 알고리즘 중 시간이 더 빠른 알고리즘을 판별하기 위해 시간 복잡도를 계산해보자.

첫 번째 함수부터 시작해보면 시작이 total의 선언이다. 시간 복잡도에서 값의 선언, 대입, 연산은 모두 1로 취급된다. 이는 어떤 상황에서도 연산이 한 번 일어나기 때문이다.

다음은 for문이다. for문의 반복 횟수는 매개변수를 참조한다. let i = 1에서 1, i <= n에서 n, 마지막으로 i++가 n번 일어나므로 2n이라고 볼 수 있다. 반복문 내의 total += i는 +=연산이므로 2라고 볼 수 있는데, 이것이 n번 만큼 반복되므로 2n이라고 본다면, 최종적으로 첫 번째 알고리즘은 5n + 2 이라고 볼 수 있다.

두 번째 함수는 시간 복잡도가 *, +, / 3개의 연산이 있으므로 3이다. 따라서 두 번째 함수가 값이 무한히 증가할 때 두 번째 함수가 월등히 빠르게 결과를 반환한다.

Big O 표기법

어떤 알고리즘이 가지고 있는 최악의 시간복잡도를 나타내는 표기법이다. 위 방법처럼 5n + 2로 표현할 수 있지만, 가장 높은 실행 시간만 표기하여 대략적인 실행속도만 추상적으로 보는 것이다.

첫 번째 함수의 시간 복잡도는 5n + 2이다. 이를 Big O로 나타내면 O(n)이 된다. 두 번째 함수는 3으로 상수다. 상수는 O(1)로 표현한다.

각 Big-O의 실행 속도의 차이를 한 눈에 볼 수 있는 그림을 첨부한다.

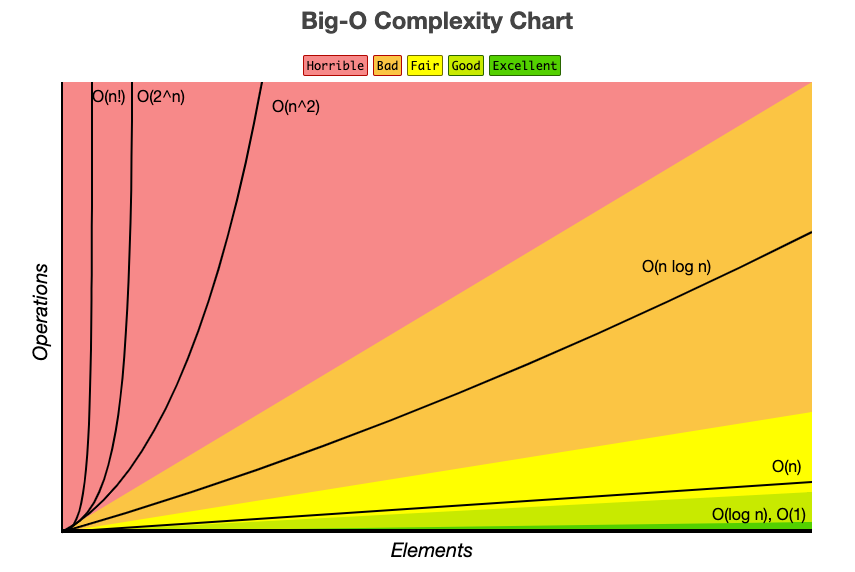
공간 복잡도

입력을 제외하고 알고리즘이 얼마나 메모리를 차지하는 지 계산하는 것이지만, 현재는 거의 고려하지 않는 것 같다. 대략적인 규칙은 변수 선언은 상수이고, 문자열, 배열, 객체는 O(N)이라는 규칙 등이 있다.

참고 자료

What is Big O Notation Explained: Space and Time Complexity