다익스트라(Dijkstra)
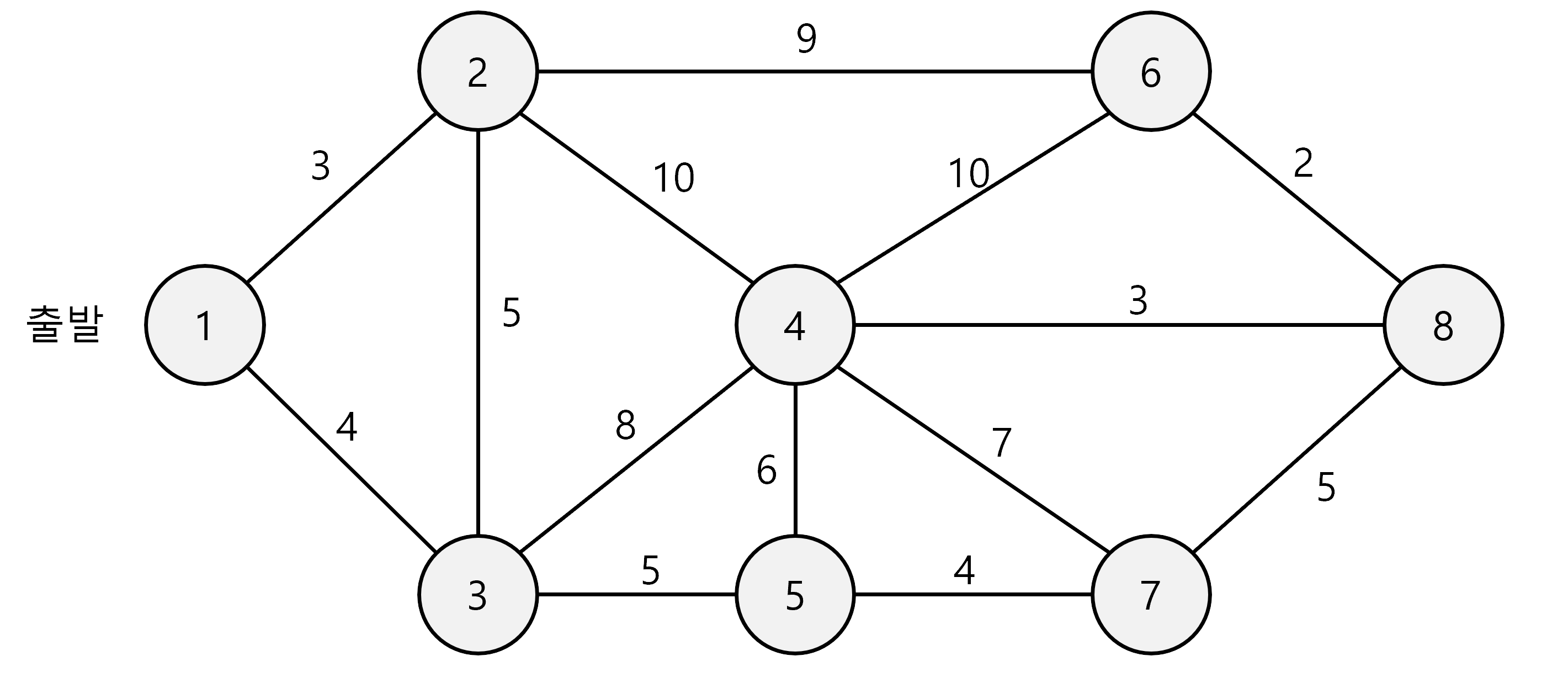
위 그래프의 출발 정점에서 모든 정점으로의 최단 거리를 구한다고 가정해보자. 이를 특정 목적지까지의 최단 경로를 구하기 쉬운 BFS로 해결하려고 한다면 가중치가 다를 경우 각 경로의 비용을 비교하고 가지치기를 수행하는 것이 어렵다.
그 이유는 BFS는 단순히 모든 경로의 가중치가 똑같다는 가정을 하여 가능한 모든 경로를 탐색하면서 가중치의 최소 비용을 따지는 것인데, 가중치가 다른 상황에서는 경로의 깊이(거쳐간 노드 또는 배열의 횟수)가 반드시 최소 비용을 보장하지 않기 때문이다.
다익스트라
이를 해결하기 위한 알고리즘으로 다익스트라 알고리즘이 있다. 다익스트라는 단일한 시작점에서 다른 모든 정점까지의 최단 경로를 계산한다. 이 알고리즘을 적용할 때 고려해야 할 점은 주어진 간선의 가중치에 음수가 없어야 한다는 것이다.
참고로 음수 가중치 간선이 존재할 경우에는 벨만-포드 알고리즘을, 모든 정점에서 소요되는 최단 경로를 구하고 싶다면 플로이드 워셜 알고리즘을 사용하는 것이 효율적이고, 나는 잘 몰랐지만 명확한 도착지가 정의된 경우에는 A* 알고리즘이 좋다고 한다. 앞서 언급한 알고리즘에 대해서 순차적으로 학습 및 정리할 것이다.
구현
그래프 구현
위와 같은 그래프를 구현하기 위해서 간이 노드 그래프를 구성하도록 하자.
class Node implements Comparable<Node> {
int to;
int weight;
Node next;
Node(int to, int weight, Node next) {
this.to = to;
this.weight = weight;
this.next = next;
}
@Override
public int compareTo(Node o) {
return Integer.compare(this.weight, o.weight);
}
}
Comparable<>은 우선순위 큐를 구현할 때 Comparator<>를 구현하기 귀찮아서 미리 구현을 해두었다. 정렬 기준은 현재 노드가 가진 가중치(구현 시에는 가중치의 합이 된다.)의 오름차순으로 정렬 기준을 설정한다. 그리고 입력은 아래와 같다.
Node[] graph = new Node[9];
graph[1] = new Node(2, 3, new Node(3, 4, null));
graph[2] = new Node(6, 9, new Node(3, 5, new Node(4, 10, null)));
graph[3] = new Node(2, 5, new Node(4, 8, new Node(5, 5, null)));
graph[4] = new Node(2, 10, new Node(3, 8, new Node(5, 6, new Node(7, 7, new Node(6, 10, new Node(8, 3, null))))));
graph[5] = new Node(3, 5, new Node(4, 6, new Node(7, 4, null)));
graph[6] = new Node(2, 9, new Node(4, 10, new Node(8, 2, null)));
graph[7] = new Node(4, 7, new Node(5, 4, new Node(8, 5, null)));
graph[8] = new Node(4, 3, new Node(6, 2, new Node(7, 5, null)));
입력받기 귀찮아서 직접 하드코드 했는데 이럴 줄 알았으면 입력 받아서 처리할 걸 그랬다…
최단 경로를 저장하는 배열 구성
최단 경로를 탐색하기 위해서는 우선 현재 정점의 최단 경로를 저장하고 있는 배열을 만들어야 한다. 또한 만들어진 최단 경로 배열을 가중치의 합이 도달할 수 없는 최대 값으로 미리 사전 세팅을 해둬야 한다. 여기서는 편하게 Integer.MAX_VALUE로 설정하도록 하겠다.
int[] dist = new int[9];
Arrays.fill(dist, Integer.MAX_VALUE);
최단 경로 탐색
최단 경로를 탐색하기 위해서 우선순위 큐를 이용하자. 다익스트라의 종료 조건은 우선 순위 큐에 노드가 더 이상 남아있지 않을 때 종료된다.
Queue<Node> pq = new PriorityQueue<>();
pq.offer(new Node(1, 0, null));
dist[1] = 0;
while(!pq.isEmpty()) {
Node cur = pq.poll();
for (Node node = graph[cur.to]; node != null; node = node.next) {
int nextWeight = node.weight + cur.weight;
if (dist[node.to] < nextWeight) continue;
dist[node.to] = nextWeight;
pq.offer(new Node(node.to, nextWeight, null));
}
}
이렇게 다익스트라를 구현할 수 있게 된다. 그리고 이 알고리즘을 자세히 살펴보면 크루스칼 알고리즘과 매우 유사하다는 것을 볼 수 있다. 두 알고리즘 모두 우선순위 큐를 사용해 가장 작은 가중치를 가진 요소를 우선적으로 처리한다는 공통점이 있다.
하지만, 다익스트라 알고리즘은 단일 출발점에서 모든 정점으로의 최단 경로를 찾는 데 사용되며, 크루스칼 알고리즘은 최소 비용 신장 트리(MST)를 찾는 데 사용된다는 차이점이 있다. 따라서 두 알고리즘은 문제 해결의 목적과 적용 방식에서 차이가 있지만, 탐욕적 접근법을 사용해 최적의 결과를 도출한다는 점에서 매우 비슷한 구조를 가지고 있다.
전체 코드
import java.util.*;
public class Main {
public static void main(String[] args) {
Node[] graph = new Node[9];
graph[1] = new Node(2, 3, new Node(3, 4, null));
graph[2] = new Node(6, 9, new Node(3, 5, new Node(4, 10, null)));
graph[3] = new Node(2, 5, new Node(4, 8, new Node(5, 5, null)));
graph[4] = new Node(2, 10, new Node(3, 8, new Node(5, 6, new Node(7, 7, new Node(6, 10, new Node(8, 3, null))))));
graph[5] = new Node(3, 5, new Node(4, 6, new Node(7, 4, null)));
graph[6] = new Node(2, 9, new Node(4, 10, new Node(8, 2, null)));
graph[7] = new Node(4, 7, new Node(5, 4, new Node(8, 5, null)));
graph[8] = new Node(4, 3, new Node(6, 2, new Node(7, 5, null)));
int[] dist = new int[9];
Arrays.fill(dist, Integer.MAX_VALUE);
Queue<Node> pq = new PriorityQueue<>();
pq.offer(new Node(1, 0, null));
dist[1] = 0;
while(!pq.isEmpty()) {
Node cur = pq.poll();
for (Node node = graph[cur.to]; node != null; node = node.next) {
int nextWeight = node.weight + cur.weight;
if (dist[node.to] < nextWeight) continue;
dist[node.to] = nextWeight;
pq.offer(new Node(node.to, nextWeight, null));
}
}
System.out.println(Arrays.toString(dist));
}
}
class Node implements Comparable<Node> {
int to;
int weight;
Node next;
Node(int to, int weight, Node next) {
this.to = to;
this.weight = weight;
this.next = next;
}
@Override
public int compareTo(Node o) {
return Integer.compare(this.weight, o.weight);
}
}
댓글남기기