그래프
그래프
완전 탐색을 알아보기 전에 우선 그래프를 알아봐야 한다. 그래프는 어떤 정점이 존재하고, 해당 정점을 선으로 연결한 구조를 말한다. 이때 정점을 연결한 선을 간선이라고 하며, 간선의 방향 유무에 따라서 방향 그래프 무방향(양방향) 그래프로 나누어지게 된다. 또한 간선은 각자의 가중치(이동하는 데 소모되는 비용 또는 거리)를 가질 수 있다.
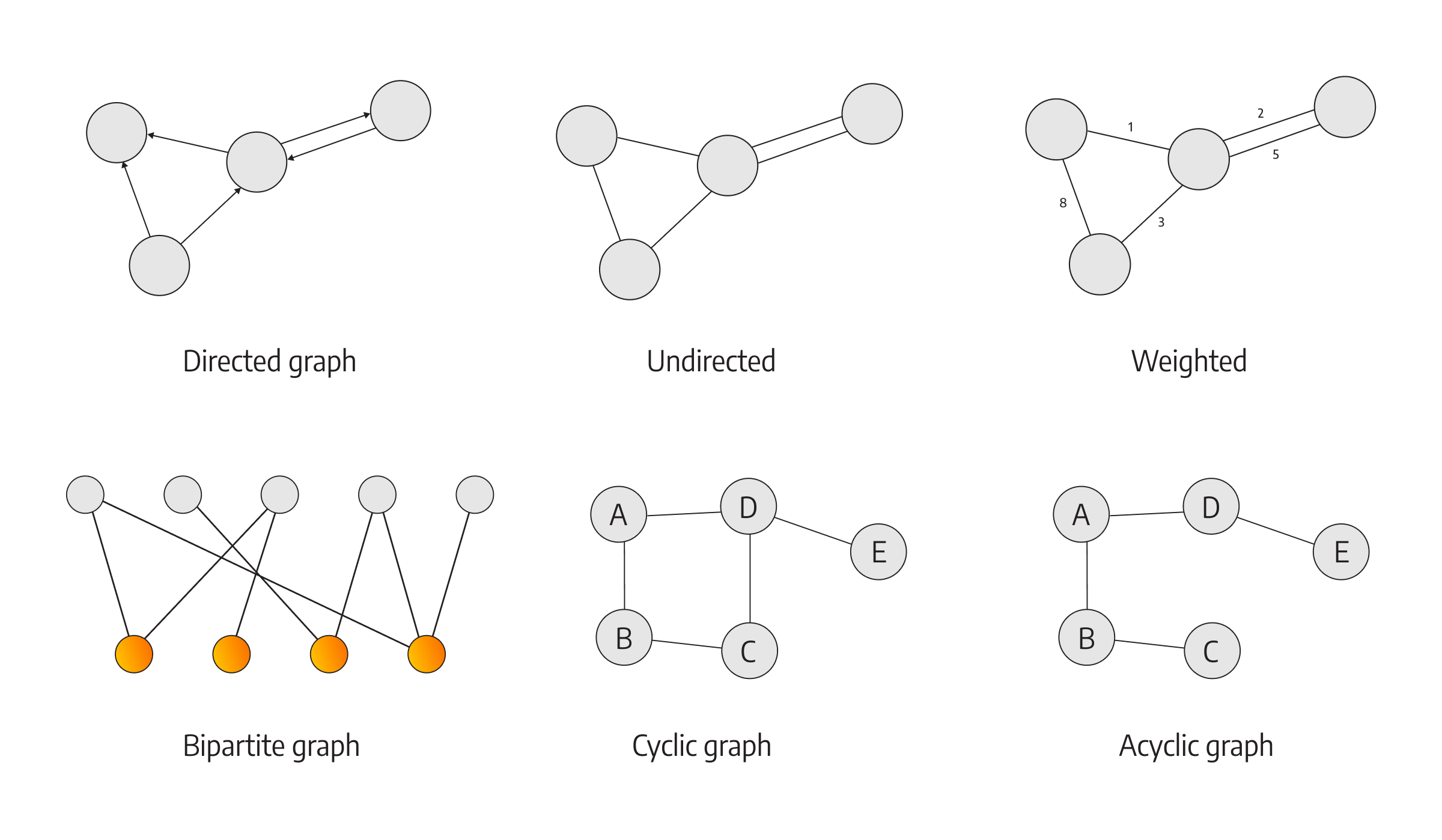
트리 vs 그래프
트리 역시 그래프의 형태 중 하나로, 순환이 없는 연결 그래프 구조를 띄는 것으로 이해하면 된다. 트리와 그래프의 차이를 나타내는 표를 첨부한다.

그래프의 표현
그래프 관련 알고리즘 문제에서 일반적으로 그래프의 입력은 정점의 개수와 두 정점의 연결관계를 표현하는 식으로 주어진다.
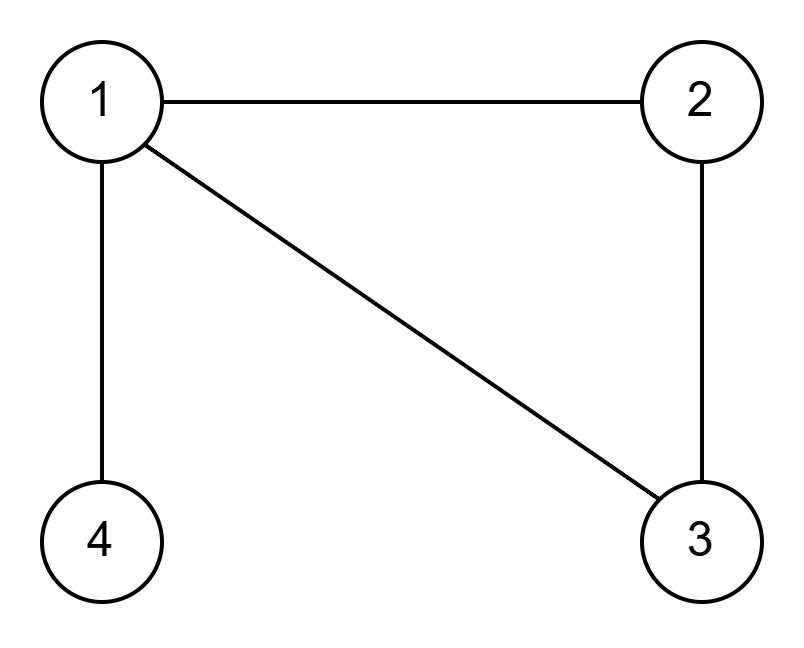
위 무방향 그래프가 주어졌을 때의 입력은 다음과 같다.
4
1 2
1 3
1 4
2 3
이렇게 입력이 주어졌을 때, 그래프를 구현하는 다양한 방법을 살펴보자.
인접 행렬
인접 행렬은 그래프를 배열을 통하여 가장 단순하게 표현하는 것이다. 가중치가 없는 경우에는 boolean 배열로 구현하기도 하며, 가중치가 존재하는 경우에는 int 배열로 구현한다. 여기서는 방향 그래프 또한 고려하여 int 배열로 구현하여 두 정점의 연결 관계를 0과 1로 표현해보겠다.
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
int N = Integer.parseInt(br.readLine());
int[][] graph = new int[N][N];
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine(), " ");
int from = Integer.parseInt(st.nextToken()) - 1;
int to = Integer.parseInt(st.nextToken()) - 1;
graph[from][to] = 1;
// 무방향 그래프의 경우
graph[to][from] = 1;
}
무방향 그래프에서는 1번 정점에서 2번 정점으로 갈 수 있다고 한다면, 그 반대로 2번 정점에서 1번 정점으로의 이동 또한 가능하다는 것이다. 따라서 두 정점을 출발지와 목적지라고 한다면, 출발지와 목적지의 인접행렬에 모두 표시를 해줘야 한다. 반대로 방향 그래프는 출발지의 인접행렬에만 표시를 해주면 될 것이다.
참고로 대부분의 문제에서는 입력값을 제시할 때 배열의 인덱스 번호를 고려해주지 않는다는 것을 유의해야 한다. 따라서 문제에 따라서 입력값을 적절하게 처리해야 할 것이다. 아무튼 위 코드를 통해 구현한 무방향 인접행렬 그래프를 보면 다음과 같다.
[0, 1, 1, 1]
[1, 0, 1, 0]
[1, 1, 0, 0]
[1, 0, 0, 0]
인접 리스트
인접 리스트는 배열이 아닌 리스트 자료구조를 통하여 구현하는 방법이다. 이 방법은 두 정점 사이의 연결 관계를 해당 리스트에 추가하는 방식이다. 탐색을 한다고 가정했을 때 인접 행렬에 비해서 탐색 속도가 더 빠를 수 있다. 정점간의 연결 관계만 표시하기 때문이다. 코드를 통해 살펴보자.
List<Integer>[] graph = new List[N];
// 인접 리스트 초기화
for (int i = 0; i < N; i++) graph[i] = new ArrayList<>(N);
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine(), " ");
int from = Integer.parseInt(st.nextToken()) - 1;
int to = Integer.parseInt(st.nextToken()) - 1;
graph[from].add(to);
// 무방향 그래프의 경우
graph[to].add(from);
}
인접 리스트를 출력해보면 다음과 같다.
[1, 2, 3]
[0, 2]
[0, 1]
[0]
마찬가지로 방향 그래프인 경우 출발지에 해당되는 인접 리스트에만 목적지를 추가하면 된다.
가중치가 존재하는 경우
하지만 만약에 그래프에 가중치가 있는 경우에는 말이 달라진다. 위 그래프에서 가중치를 추가하여 살펴보자
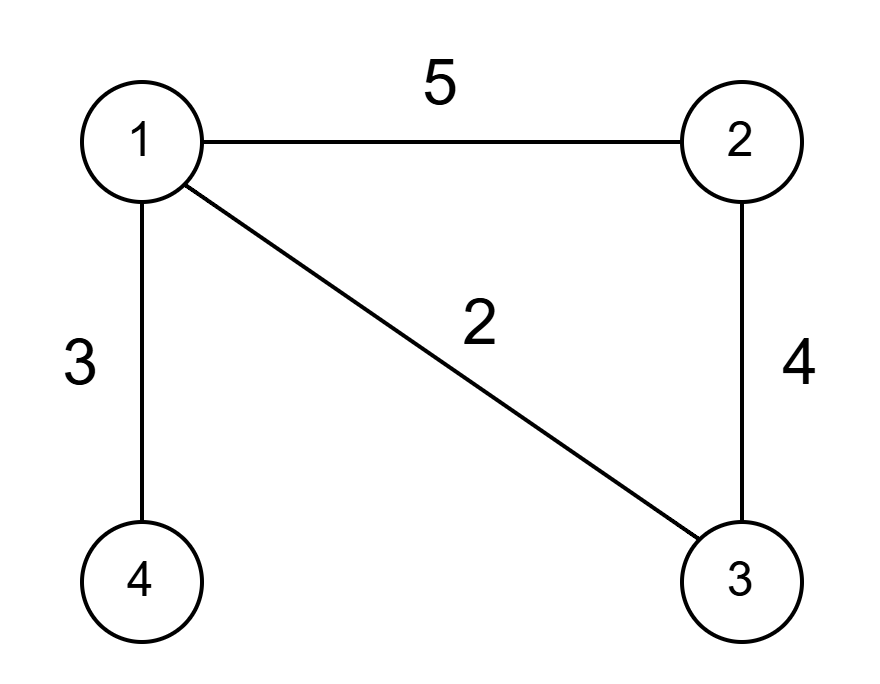
이 경우 입력값은 다음과 같다.
4
1 2 5
1 3 2
1 4 3
2 3 4
가중치가 있는 경우에 인접 행렬에서는 가중치를 행렬의 원소로 표시해주면 되지만 인접 리스트에서는 목적지와 가중치를 저장하는 배열 또는 객체를 저장하도록 해야 한다.
int N = Integer.parseInt(br.readLine());
List<int[]>[] graph = new List[N];
for (int i = 0; i < N; i++) graph[i] = new ArrayList<>(N);
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine(), " ");
int from = Integer.parseInt(st.nextToken()) - 1;
int to = Integer.parseInt(st.nextToken()) - 1;
int weight = Integer.parseInt(st.nextToken());
graph[from].add(new int[] {to, weight});
graph[to].add(new int[] {from, weight});
}
또는
class Node {
int to;
int weight;
public Node(int to, int weight) {
this.to = to;
this.weight = weight;
}
}
이렇게 객체로 저장하고자 한다면
List<Node>[] graph = new List[N];
graph[from].add(new Node(to, weight));
graph[to].add(new Node(from, weight));
이런 식으로 인접 리스트를 구현할 수 있다.
노드 기반 연결 리스트
이 방법은 앞서 인접 리스트를 구현할 때 만든 객체를 조금 변형하여 객체끼리 참조하는 식으로 정점 사이의 연결 관계를 구현하는 것이다. 무방향 그래프를 연결 리스트를 통해 구현하면 다음과 같다.
class Node {
int to;
Node next;
public Node(int to, Node next) {
this.to = to;
this.next = next;
}
@Override
public String toString() {
return "Node [to=" + to + ", next=" + next + "]";
}
}
int N = Integer.parseInt(br.readLine());
Node[] graph = new Node[N];
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine(), " ");
int from = Integer.parseInt(st.nextToken()) - 1;
int to = Integer.parseInt(st.nextToken()) - 1;
graph[from] = new Node(to, graph[from]);
graph[to] = new Node(from, graph[to]);
}
이를 toString()을 재정의하여 출력한 결과는 다음과 같다.
Node [to=3, next=Node [to=2, next=Node [to=1, next=null]]]
Node [to=2, next=Node [to=0, next=null]]
Node [to=1, next=Node [to=0, next=null]]
Node [to=0, next=null]
그래프가 가중치를 가진다면 다음과 같이 객체를 구성하면 된다. 입력값 형식은 앞서 가중치가 있는 인접 리스트를 구현할 때 사용한 입력값을 사용한다.
class Node {
int to;
int weight;
Node next;
public Node(int to, int weight, Node next) {
this.to = to;
this.weight = weight;
this.next = next;
}
}
// weight를 입력 받았다고 가정
graph[from] = new Node(to, weight, graph[from]);
graph[to] = new Node(from, weight, graph[to]);
개인적으로 특별한 경우가 아니라면 연결 리스트를 응용하여 구현하는 방법을 선호한다. 하지만 몇몇 문제에서 인접 행렬이나 인접 리스트를 이용하여 구현해야 편리한 경우가 존재한다. 따라서 하나의 방법이 아닌 모든 방법을 숙지해 놓고, 문제에 따라서 적절하게 필요한 그래프 구현 방법을 선택하는 것이 좋다.
댓글남기기