Sehako

어느 개발자의 기록 공간

순열

서로 다른 n개중 r개를 순서를 고려하여 택하는 것으로 $_nP_r$이라고 표현합니다. $_nP_r$은 다음과 같은 식이 성립합니다.

\[_nP_r = n \times (n - 1) \times (n - 2) \times ... \times (n - r + 1)\]

$_nP_n$은 일반적으로 $n!$이라고 표기하며 팩토리얼이라고 합니다.

\[_nP_r = n \times (n - 1) \times (n - 2) \times ... \times 2 \times 1\]

순열은 코드로 구현하면 $O(n!)$의 시간복잡도를 가집니다. 따라서 만약에 N의 개수가 10개이고 이 중 10개를 선택하는 경우는 $O(10!)$이 되는데 이 값은 3,628,800입니다.

일반적으로 알고리즘 문제를 풀 때 1초에 $10^8$의 계산을 한다고 가정합니다. 따라서 최대한 보수적으로 잡는다면 n이 10 이하일 때에만 순열 알고리즘을 적용하는 것이 안전할 것이고, 11이면 39,916,800이기 때문에 다른 방법을 찾는 것이 좋을 것 같습니다.

구현

반복문

만약 n개의 숫자 중에서 3개의 숫자를 순서를 고려하여 선택하면 다음과 같은 코드가 완성됩니다.

for (int i = 0; i < N; i++) {
    // 두 번째 원소 선택
    for (int j = 0; j < N; j++) {
        // 첫 번째 원소와 중복되는 원소 제거
        if (i != j) {
            // 세 번째 원소 선택
            for (int k = 0; k < N; k++) {
                // 첫 번째 및 두 번째 원소와 중복되는 원소는 뽑지 않음
                if (k != i && k != j) {
                    System.out.printf("%d %d %d\n", data[i], data[j], data[k]);
                }
            }
        }
    }
}

하지만 이 코드는 가변적이지 않습니다. 저 코드는 주어진 배열(n개의 숫자)에서 무조건 3개만 선택할 수 있습니다. 반복문으로 순열을 구현하려면 반복문의 중첩 개수에 따라서 r의 값이 정해지게 되는 것입니다.

구현

재귀

따라서 재귀 호출을 통해서 순열을 구현하는 것이 일반적입니다. 3개를 선택하는 순열을 재귀로 구현한 코드를 통해 확인해보겠습니다.

int[] data = {1, 2, 3};

// 3개를 선택하는 순열 예시
void permutation(int depth) {
    // 기저 조건 (재귀 탈출 조건)
    //배열은 0부터 시작하므로 R-1개가 모든 원소를 뽑은 상황.
    //depth가 R과 동일한 상황은 순열 하나의 모든 원소를 다 뽑은 상황
    if(depth == 3) return;

    for (int i = 0; i <N; i++) {
        //중복 검사
        if(ch[i]) continue;
        // 중복이 되면 안되므로 boolean 배열을 통해 중복값을 관리
        ch[i] = true;
        // 유도 부분(재귀 호출 부분)
        permutation(depth + 1);
        // 재귀 호출을 빠져나오면 해당 숫자는 선택을 끝난 상태이므로 중복값 체크 해제
        ch[i] = false;
    }
}

이렇게 순열을 구성하면 depth의 기저 조건만 조정해주면 됩니다.

재귀 구조 시각화 하기

재귀 함수를 처음 접하면 코드가 잘 이해가 안됩니다. 개인적으로 재귀 함수의 호출을 트리 형식으로 그려나가는 식으로 학습했을 때 도움이 많이 되었습니다. 위 순열 코드를 기반으로 재귀 함수의 호출 구조를 시각화 하면 다음과 같습니다.

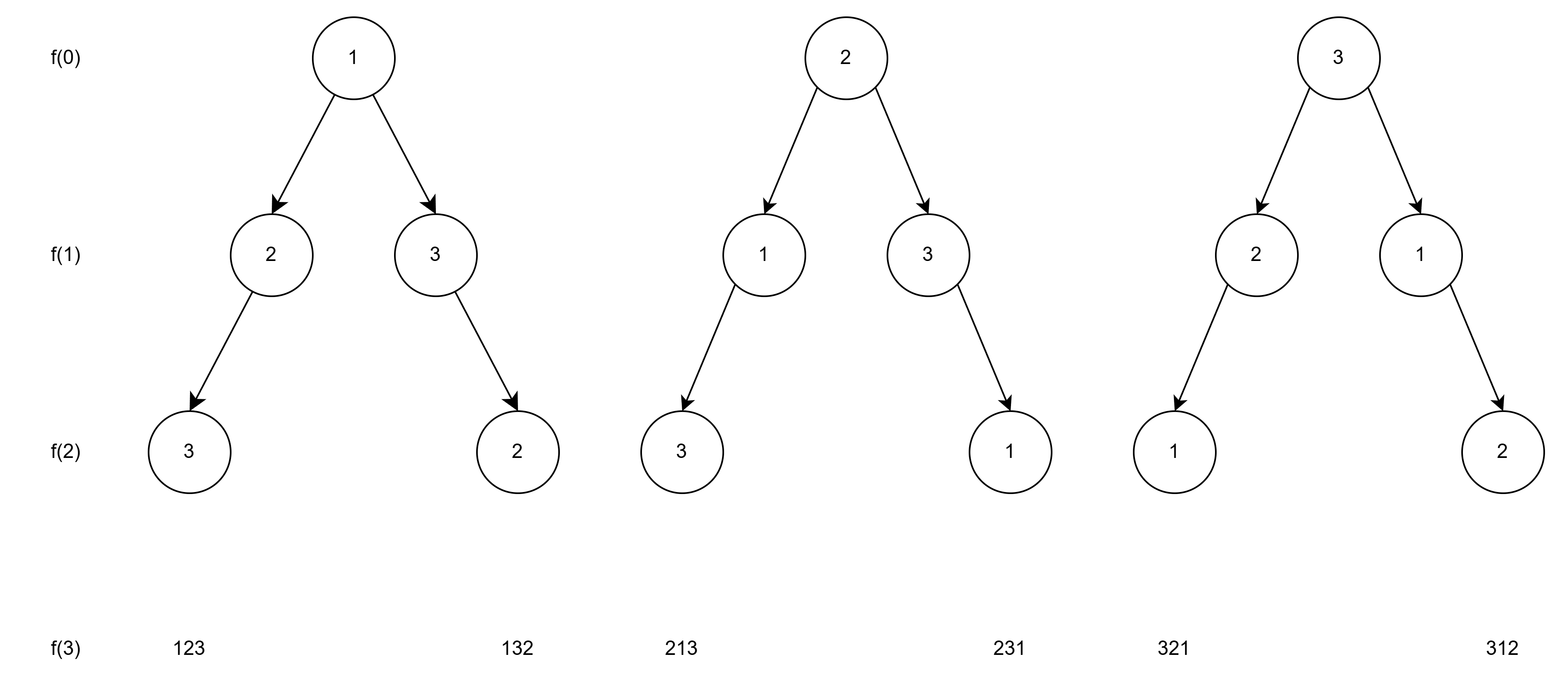
image.png

이렇게 해서 $3! = 6$개의 순열이 나오는 것을 확인할 수 있습니다. 지금은 간단한 구조라 모양이 단순하지만 복잡한 재귀일수록 이해가 잘 안되면 그려나가는 것이 도움이 많이 되므로 그려보는 것을 추천합니다.

비트마스킹

void permutation(int depth, int flag) {
    if(depth == R) return;

    //원소를 선택
    for (int i = 0; i < N; i++) {
        count++;
        //중복 검사
        if((flag & 1 << i) != 0) continue;
        permutation(depth+1, flag | 1 << i);
    }
}

비트 연산을 이용한 순열의 예시입니다. 초기 flag의 값은 0으로 이는 2진수로 0000입니다. 이때 1이 선택 된다면 0010으로 바뀌고, 다음 유도 부분으로 넘어갑니다. 그러면 다음 재귀 호출에서는 flag값이 0010이 되고, 이는 중복 검사 부분에서 AND연산 수행 시 0이 도출되지 않습니다.

이 방법의 좋은 점은 boolean[]을 따로 둘 필요가 없고, 단순하게 넘겨받는 인자를 통해서 중복을 체크하므로 현재 flag값에 OR연산을 수행한 값만 넘겨주면 됩니다.

교환 순열

이 방법은 n개의 숫자에서 n개를 선택하는 $_nP_n(n!)$ 상황일 때, 원본 배열만으로 순열을 구성할 수 있는 방법입니다.

int[] data = {1, 2, 3, 4, 5};

void permutation(int depth) {
    if(depth == data.length - 1) return;
    for (int i = depth; i < N; i++) {
        swap(i, depth);
        permutation(depth + 1);
        swap(i, depth);
    }
}

void swap(int a, int b) {
    int temp = data[a];
    data[a] = data[b];
    data[b] = temp;
}

중복 순열

각 상황의 경우의 수가 앞선 상황에 영향을 받지 않는 경우에는 중복 순열을 이용한 재귀 호출 구현이 필요합니다. 수식으로 보면 다음과 같습니다.

\[_n \Pi _r = n \times n \times ... \times n = n^r\]

구현은 간단하게 순열에서 선택 여부에 관한 플래그 변수를 없애면 됩니다.

void permutation(int depth) {
    if(depth == 3) return;

    for (int i = 0; i <N; i++) {
        data[depth] = input[i];
        permutation(depth + 1);
    }
}

댓글남기기

참고