백엔드 개발자 지망생

이론

주어진 배열에서 특정 구간의 합이나 최소값 / 최대값 등을 손쉽게 조회하고, 업데이트 하는 데 사용하는 자료구조이다. 구간의 합에 대해서는 일반적으로 누적합을 많이 사용한다. 이는 주어진 구간을 $O(1)$에 구할 수 있지만, 만약에 주어진 배열의 특정 인덱스의 값을 변경하면 이에 대한 업데이트를 해야 하기 때문에 $O(N)$의 시간이 소요된다.

세그먼트 트리는 이 두 연산을 모두 $O(logN)$으로 처리할 수 있다. 따라서 세그먼트 트리를 사용하는 기준은 다음과 같을 것이다.

  • 문제가 구간의 합 이외에도 구간의 합을 업데이트해야 하는가?
  • 문제가 구간의 합이 아닌 구간의 최소값 / 최대값 등을 구해야 하는가?

기본 구상은 매우 간단한데, 전체 10개의 배열 요소에 대해서 구간합을 구하는 세그먼트 트리를 그림으로 표현하면 다음과 같다.

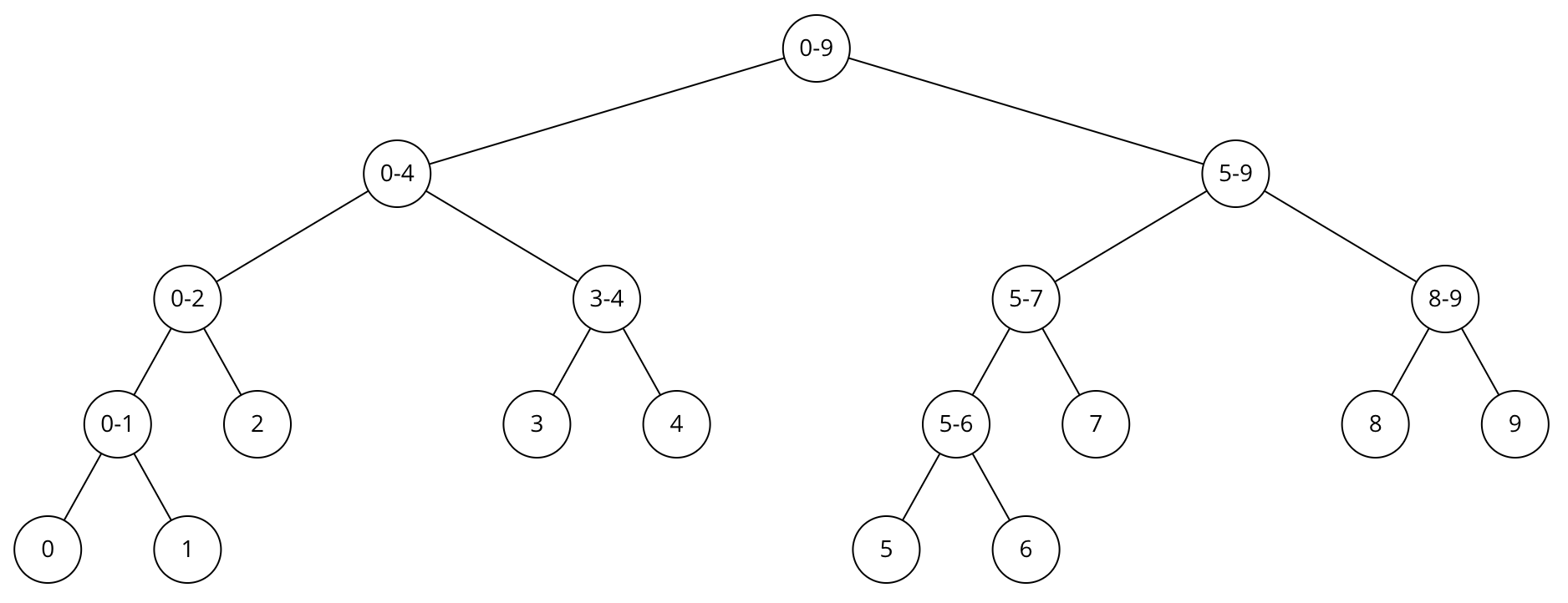
image.png

세그먼트 트리는 이진 트리의 형태를 가진다. 만약 주어진 배열의 개수가 2의 제곱꼴인 경우에는 완전 이진 트리의 형태가 된다. 리프 노드에는 배열의 수가 담겨져 있고, 부모 노드에는 두 노드에 대한 연산을 수행한 결과가 담겨져 있는 것을 확인할 수 있다.

알고리즘 구현

구간합에 대한 세그먼트 트리를 만들어보자. 이 코드를 활용하면 구간 합 구하기 문제를 해결할 수 있다.

세그먼트 트리 크기 결정

세그먼트 트리를 구성하려면 원본 배열의 크기에 따라 트리의 높이와 필요한 노드 수를 먼저 결정해야 한다.

세그먼트 트리는 완전 이진 트리(Complete Binary Tree) 구조를 사용하므로, 레벨이 하나 증가할 때마다 노드 수가 2배씩 증가한다.

  • 레벨 0 : 1개의 노드(루트)
  • 레벨 1 : 2개의 노드
  • 레벨 2 : 4개의 노드
  • 레벨 3 : 8개의 노드

이러한 특성에 대해서 원본 배열 크기 N에 대해서 다음 부등식이 성립된다.

\[2^{h-1} \lt N \le 2^h\]

여기서 $log_2$를 취하면 다음과 같다.

\[h-1\lt log_2(N) \le h \quad (h \ge 1) \\ \therefore \, ⌈log_2(N)⌉=h\]

그리고 리프 노드 L의 개수는 트리의 높이에 따라서 다음과 같이 이루어진다.

\[L=2^h\]

이에 대해서 전체 노드 수 T는 각 깊이 별 노드의 개수를 합친 것이므로 다음과 같고,

\[T=1+2+4+...+2^h\]

이는 등비수열의 공식에 따라서 다음과 같이 표현할 수 있다.

\[T=\frac{2^{h + 1} - 1}{2 - 1} = 2^{h+1}-1\]

여기서 루트 노드 인덱스가 1부터 시작하기 때문에 세그먼트 트리에 대한 전체 배열 크기 S는 다음과 같이 설정하면 된다.

\[S=T=2^{h+1}\]

이를 자바 코드로 표현하면 두 가지 방법을 사용할 수 있다.

int n = arr.length;

// 방법 1. Math 클래스를 활용하여 계산
int h = (int) Math.ceil(Math.log(n) / Math.log(2));
int treeSize = (int) Math.pow(2, h + 1);
long[] tree = new long[treeSize];

// 방법 2. Integer 클래스 + 비트 연산으로 계산
// h = ceil(log2(n))
int h = (n <= 1) ? 0 : 32 - Integer.numberOfLeadingZeros(n - 1);

int treeSize = 1 << (h + 1);
long[] tree = new long[treeSize];

두 번째 방법이 성능이 좀 더 빠르다고는 하는데 이걸 실제 코딩 테스트 환경에서 작성할 수 있을까 싶어서 나는 다음과 같이 트리 배열의 크기를 구하는 코드를 사용하였다.

public class SegmentTree {
	private final long[] tree;

	public SegmentTree(int[] arr) {
		int n = arr.length;

		int h = (int) Math.ceil(Math.log(n) / Math.log(2));

		tree = new long[1 << (h + 1)];
	}
}

참고로 이러한 높이 계산이 난해하다면 원본 배열 크기에 4를 곱하는 방식을 사용할 수도 있다.

public class SegmentTree {
	private final long[] tree;

	public SegmentTree(int[] arr) {
		int n = arr.length;
		tree = new long[4 * n];
	}
}

코드가 간단하기 때문에 틀릴 일은 없지만 메모리를 넉넉하게 잡는 방식이므로 메모리 낭비에 대해서는 주의해햐 한다.

트리 초기화

트리 초기화는 재귀적인 방식으로 구현하면 된다.

private void build(long[] arr, int n, int s, int e) {
	if (s == e) {
		tree[n] = arr[s];
		return;
	}

	build(arr, n * 2, s, (s + e) / 2);
	build(arr, n * 2 + 1, (s + e) / 2 + 1, e);

	tree[n] = tree[n * 2] + tree[n * 2 + 1];
}

이 메서드를 트리 배열을 생성할 때 원본 배열과 함께 다음과 같이 호출하면 된다.

public SegmentTree(int[] org) {
	// ...
	build(org, 1, 0, n - 1);
}

구간 합 구하기

public long query(int n, int s, int e, int l, int r) {
	if (s > r || e < l) return 0L;
	if (l <= s && e <= r) {
		return tree[n];
	}

	long leftQuery = query(n * 2, s, (s + e) / 2, l, r);
	long rightQuery = query(n * 2 + 1, (s + e) / 2 + 1, e, l, r);

	return leftQuery + rightQuery;
}

노드에 저장된 구간이 [s, e]이고, 합을 구해야 하는 구간이 [l, r]이면 4가지의 경우가 존재한다.

  1. [l, r]과 [s, e]가 겹치지 않는 경우
  2. [l, r]가 [s, e]를 완전히 포함하는 경우
  3. [s, e]가 [l, r]를 완전히 포함하는 경우
  4. [l, r]와 [s, e]가 겹쳐져 있는 경우

첫 번째 경우에는 탐색을 이어나갈 이유가 없기 때문에 0을 반환한다.

두 번째 경우에서도 탐색을 이어나갈 이유가 없다. 구하고자 하는 범위가 저장된 구간을 포함하고 있기 때문이다. 따라서 tree[n], 즉 현재 노드 값을 반환하면 된다.

나머지 경우에서는 현재 노드의 왼쪽과 오른쪽 하위 노드를 루트로 하는 트리에서 탐색을 이어나간다.

값 업데이트하기

값을 업데이트하는 방법은 두 가지가 존재한다. 하나씩 알아보도록 하자.

차이 계산 후 인덱스 범위에 해당하는 수 업데이트

원본 배열의 인덱스를 변경하는 경우, 해당 인덱스를 포함하는 노드에서 차이점만 연산하면 된다. 원래 배열의 값이 arr[idx]이고, 변경된 수와 기존의 수가 diff라고 했을 때 코드는 다음과 같다.

public void update(int n, int s, int e, int idx, long diff) {
	if (idx < s || idx > e) return;
	tree[n] += diff;

	if (s == e) return;

	update(n * 2, s, (s + e) / 2, idx, diff);
	update(n * 2 + 1, (s + e) / 2 + 1, e, idx, diff);
}

이때 다음 두 가지의 상황이 발생한다.

  1. idx가 [s, e]에 포함되는 경우
  2. 포함되지 않는 경우

1번 경우에만 재귀 호출을 진행하다가, s와 e가 같아지면 더 이상 업데이트를 할 필요가 없으므로 재귀 호출을 끝낸다.

리프 노드에 차이점 반영 후 각 노드의 합 업데이트

이 방법은 리프 노드까지 탐색을 하고, 해당 노드에서 주어진 차이점을 업데이트한 이후 재귀 호출이 끝날때마다 각 노드를 업데이트하는 방법이다.

public void update(int n, int s, int e, int idx, long diff) {
	if (idx < s || idx > e) return;
	if (s == e) {
		tree[n] += diff;
		return;
	}
	update(n * 2, s, (s + e) / 2, idx, diff);
	update(n * 2 + 1, (s + e) / 2 + 1, e, idx, diff);

	tree[n] = tree[n * 2] + tree[n * 2 + 1];
}

두 방법 모두 시간복잡도는 같으므로 편한 방법을 사용하도록 하자.

범위 값 업데이트하기 (Lazy Propagation)

만약에 한 번에 K 범위 만큼의 특정 원소들을 업데이트 연산을 진행한다면, 업데이트의 시간복잡도인 $O(logN)$에 추가로 K번의 연산이 수행되므로 $O(KlogN)$의 시간이 소요된다. 이는 배열에서 연산을 활용하는 경우인 $O(N)$보다 더 많은 시간을 요구하는 것이다.

이를 개선하기 위해서 범위를 가지는 업데이트 연산에 대해서 느리게 업데이트되는 세그먼트 트리를 활용할 수 있다. 느리게 업데이트되는 세그먼트 트리는 업데이트를 위한 별도의 트리를 하나 만들고, 여기에 각 노드가 업데이트되어야 하는 값을 저장해두는 기법이다. 이를 통해 구간에 대한 업데이트 연산을 $O(logN)$으로 처리할 수 있다. 코드를 통해 살펴보자.

업데이트 적용

private final long[] update;

private static void applyUpdate(int n, int s, int e) {
	if (update[n] != 0) {
		tree[n] += (e - s + 1) * update[n];

		if (s != e) {
			update[n * 2] += update[n];
			update[n * 2 + 1] += update[n];
		}

		update[n] = 0;
	}
}

update 배열에 저장된 변경 값을 반영하는 메서드이다. 이때 트리의 노드에 (e - s + 1) * update[n] 을 통해서 업데이트를 적용하는데, 이는 해당 노드가 담당하는 구간의 각 수에 더해야 하는 값이 저장되어 있기 때문에 합에는 그 구간에 포함된 수의 개수만큼 곱해서 더해야 하기 때문이다.

이후에 s와 e가 같지 않다면 현재 업데이트 값을 하위 노드로 전파시킨 다음에 현재 노드의 업데이트 값을 0으로 초기화 한다. 이 메서드를 각각 범위 업데이트와 쿼리 메서드의 시작 지점에서 호출하면 된다.

private static void updateRange(int n, int s, int e, int l, int r, long diff) {
	applyUpdate(n, s, e);
	// ...
}

private static long query(int n, int s, int e, int l, int r) {
	applyUpdate(n, s, e);
	// ...
}

범위 업데이트

private static void updateRange(int n, int s, int e, int l, int r, long diff) {
	applyUpdate(n, s, e);
	if (s > r || e < l) return;
	if (l <= s && e <= r) {
		tree[n] += (e - s + 1) * diff;

		if (s != e) {
			update[n * 2] += diff;
			update[n * 2 + 1] += diff;
		}

		return;
	}

	updateRange(n * 2, s, (s + e) / 2, l, r, diff);
	updateRange(n * 2 + 1, (s + e) / 2 + 1, e, l, r, diff);

	tree[n] = tree[n * 2] + tree[n * 2 + 1];
}

트리의 시작과 끝이 주어진 범위 이내에 존재하면 앞서 업데이트 반영 메서드와 마찬가지로 업데이트 값에 (e - s + 1)을 곱하여 트리를 업데이트하는 것을 볼 수 있다.

이후에 시작과 끝이 같지 않다면 update 배열에 업데이트 값을 전파하면서 수정해나간다.

전체 코드

세그먼트 트리를 자바로 구현한 전체 코드는 다음과 같다.

public class SegmentTree {
	private long[] tree, update;

	public SegmentTree(long[] arr) {
		int n = arr.length;
		int h = (int) Math.ceil(Math.log(n) / Math.log(2));

		tree = new long[1 << (h + 1)];
		update = new long[1 << (h + 1)];

		build(arr, 1, 0, n - 1);
	}

	private void build(long[] arr, int n, int s, int e) {
		if (s == e) {
			tree[n] = arr[s];
			return;
		}

		build(arr, n * 2, s, (s + e) / 2);
		build(arr, n * 2 + 1, (s + e) / 2 + 1, e);

		tree[n] = tree[n * 2] + tree[n * 2 + 1];
	}

	public long query(int n, int s, int e, int l, int r) {
		applyUpdate(n, s, e);
		if (s > r || e < l) return 0L;
		if (l <= s && e <= r) {
			return tree[n];
		}

		long leftQuery = query(n * 2, s, (s + e) / 2, l, r);
		long rightQuery = query(n * 2 + 1, (s + e) / 2 + 1, e, l, r);

		return leftQuery + rightQuery;
	}

	public void update(int n, int s, int e, int idx, long diff) {
		if (idx < s || idx > e) return;

		tree[n] += diff;

		if (s == e) return;

		update(n * 2, s, (s + e) / 2, idx, diff);
		update(n * 2 + 1, (s + e) / 2 + 1, e, idx, diff);
	}

	public void updateRange(int n, int s, int e, int l, int r, long diff) {
		applyUpdate(n, s, e);
		if (s > r || e < l) return;
		if (l <= s && e <= r) {
			tree[n] += (e - s + 1) * diff;

			if (s != e) {
				update[n * 2] += diff;
				update[n * 2 + 1] += diff;
			}

			return;
		}

		updateRange(n * 2, s, (s + e) / 2, l, r, diff);
		updateRange(n * 2 + 1, (s + e) / 2 + 1, e, l, r, diff);

		tree[n] = tree[n * 2] + tree[n * 2 + 1];
	}

	private void applyUpdate(int n, int s, int e) {
		if (update[n] != 0) {
			tree[n] += (e - s + 1) * update[n];

			if (s != e) {
				update[n * 2] += update[n];
				update[n * 2 + 1] += update[n];
			}

			update[n] = 0;
		}
	}

}

참고 자료

세그먼트 트리 (Segment Tree)

[Algorithm] 세그먼트 트리(Segment Tree)를 Java로 구현해보자! !(with BOJ-2042 Java로 문제풀이)

[자료구조] 세그먼트 트리 Segment Tree (Java)

느리게 업데이트되는 세그먼트 트리 (Segment Tree with Lazy Propagation)

카테고리:

업데이트:

댓글남기기

참고